Problem Set 4
Given an adjacency-list representation of a directed graph, where each vertex maintains an array of its outgoing edges (but *not* its incoming edges), how long does it take, in the worst case, to compute the in-degree of a given vertex? As usual, we use \(n\) and \(m\) to denote the number of vertices and edges, respectively, of the given graph. Also, let \(k\) denote the maximum in-degree of a vertex. (Recall that the in-degree of a vertex is the number of edges that enter it.)
- \(\Theta(n)\)
- Cannot determine from the given information
- \(\Theta(k)\)
- \(\Theta(m)\)
ANSWER: We must read all edges (or the edge not read may contribute to a in-degree count of the given vertex), so we have the time lowered bounded by \(m\).
We can compute the in-degree by just reading all edges and keep track of the in-degree count, so we have the time upper bounded by \(m\).
Therefore the solution is \(\Theta(m)\). Option 4 is correct.
Consider the following problem: given an undirected graph \(G\) with \(n\) vertices and \(m\) edges, and two vertices \(s\) and \(t\), does there exist at least one \(s-t\) path?
If \(G\) is given in its adjacency list representation, then the above problem can be solved in \(O(m + n)\) time, using BFS or DFS. (Make sure you see why this is true.)
Suppose instead that \(G\) is given in its adjacency *matrix* representation. What running time is required, in the worst case, to solve the computational problem stated above? (Assume that \(G\) has no parallel edges.)
- \(\Theta(n * m)\)
- \(\Theta(m + n\log n)\)
- \(\Theta(n^2)\)
- \(\Theta(m + n)\)
ANSWER: Option 3 is correct. For the lower bound, every time we want to find the edges adjacent to a given vertex \(u\), we have to traverse the whole array, which is of length \(n\); this happens for all the vertices. One easy way to prove the upper bound is to first build an adjacency list representation in \(\Theta(n^2)\) time, with a single scan over the given adjacency matrix and then run BFS or DFS as in the video lectures.
This problem explores the relationship between two definitions about graph distances. In this problem, we consider only graphs that are undirected and connected. The diameter of a graph is the maximum, over all choices of vertices \(s\) and \(t\), of the shortest-path distance between \(s\) and \(t\). (Recall the shortest-path distance between \(s\) and \(t\) is the fewest number of edges in an \(s-t\) path.)
Next, for a vertex \(s\), let \(l(s)\) denote the maximum, over all vertices \(t\), of the shortest-path distance between \(s\) and \(t\). The radius of a graph is the minimum of \(l(s)\) over all choices of the vertex \(s\).
Which of the following inequalities always hold (i.e., in every undirected connected graph) for the radius \(r\) and the diameter \(d\)? [Select all that apply.]
- \(r \leq \frac{d}{2}\)
- \(r \leq d\)
- \(r \geq d\)
- \(r \geq \frac{d}{2}\)
ANSWER: We need some definitions:
- Distance: The distance between two vertices \(u\) and \(v\) in a graph \(G\) is is defined as the length of a shortest path from \(u\) to \(v\) and is denoted by \(d(u,v)\). Distance on graphs is a metric and defines a metric space. Mathematically, \(d: V(G) \times V(G) \to \mathbb{Z}^* \cup {0}\), where \(V\) is the vertex set and \(\mathbb{Z}^*\) the set of positive integers.
Distance rules:
- \(d(u, v) \geq 0\) and \(d(u, v) = 0 \iff u = v\)
- \(d(u, v) = d(v, u)\)
- \(d(u, w) \leq d(u, v) + d(v, w)\)
1 and 2 should be obvious. 3 follows from the Triangle inequaity; we can use this property because distance on graphs is a metric.
-
Eccentricity: Maximum distance between a given vertex \(v\) to any other vertex \(u\) in the graph. \(e(v) = max \{d(u, v) \ \vert \ u,v \in G\}\)
-
Diameter: Maximum eccentricity. \(diam(G) = max \{e(v) \ \vert \ v \in G\}\)
-
Radius: Minumum eccentricity. \(rad(G) = min \{e(v) \ \vert \ v \in G\}\)
Example:
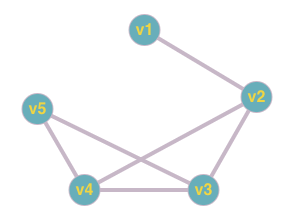
| v | e(v) |
|---|---|
| v1 | 3 |
| v2 | 2 |
| v3 | 2 |
| v4 | 2 |
| v5 | 3 |
\(diam(G) = 3, rad(G) = 2\)
- Center: The set of all such vertices for which \(e(v) = rad(G)\) make up the center of \(G\).
- Periphery: The set of all such vertices for which \(e(v) = diam(G)\) make up the periphery of \(G\).
Now, we will prove that \(rad(G) \leq diam(G) \leq 2 * rad(G)\). The first part is obvious from the definitions of radius and diameter. For the second part, consider two vertices \(u\) and \(v\) on the periphery. Consider a vertex \(w\) in the center. By distance law:
\[\begin{equation*} \begin{aligned} d(u, v) & \leq d(u, w) + d(w, v) \\ & \leq 2 * e(w) \\ \therefore diam(G) & \leq 2 * rad(G) \end{aligned} \end{equation*}\]Therefore, options 2 and 4 are correct.
Consider our algorithm for computing a topological ordering that is based on depth-first search (i.e., NOT the “straightforward solution”). Suppose we run this algorithm on a graph \(G\) that is NOT directed acyclic. Obviously it won’t compute a topological order (since none exist). Does it compute an ordering that minimizes the number of edges that go backward?
For example, consider the four-node graph with the six directed edges \((s,v),(s,w),(v,w),(v,t),(w,t),(t,s)\). Suppose the vertices are ordered \(s,v,w,t\). Then there is one backwards arc, the \((t,s)\) arc. No ordering of the vertices has zero backwards arcs, and some have more than one.
- Sometimes yes, sometimes no
- Never
- If and only if the graph is a directed cycle
- Always
ANSWER: The graph in question is shown below:
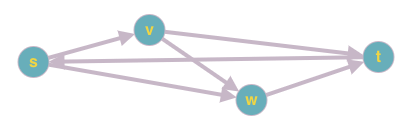
If we run DFS from vertex \(s\), there is only one backward edge \((t, s)\). But if we run DFS from \(t\), the ordering is \(w, v, s, t\), with all the edges pointing backward. Thus, option 1 is coorect.
On adding one extra edge to a directed graph \(G\), the number of strongly connected components…?
- …never decreases by more than 1 (no matter what \(G\) is)
- …never decreases (no matter what \(G\) is)
- …could remain the same (for some graphs \(G\))
- …will definitely not change (no matter what \(G\) is)
ANSWER: Consider the directed path \(1 \rightarrow 2 \rightarrow 3 \rightarrow 4\); there are four SCCs, one for each vertex. If we add an edge \(4 \rightarrow 1\), then the four SCCs merge into one; therefore, options 1, 2 and 4 are incorrect. On the other hand, adding edge \(1 \rightarrow 2\) doesn’t change anything. Thus, option 3 is correct.

Leave a comment