Recall the Partition subroutine that we used in both QuickSort and RSelect. Suppose that the following array has just been partitioned around some pivot element: \(3, 1, 2, 4, 5, 8, 7, 6, 9\). Which of these elements could have been the pivot element? (Hint: Check all that apply, there could be more than one possibility!)

  • \(4\)
  • \(2\)
  • \(3\)
  • \(5\)
  • \(9\)

ANSWER: \(4, 5 \text{ and } 9\). Since the pivot must be in it’s rightful place in the sorted array, every other element is eliminated. Each of these also satisfies the partitioning property. Options 1, 4, and 5 are correct.

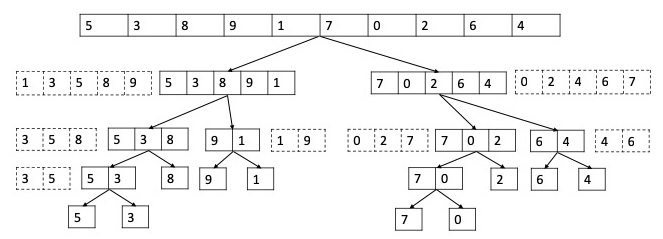
Here is an array of ten integers: \(5 3 8 9 1 7 0 2 6 4\). Suppose we run MergeSort on this array. What is the number in the 7th position of the partially sorted array after the outermost two recursive calls have completed (i.e., just before the very last Merge step)? (When we say “7th” position, we’re counting positions starting at \(1\); for example, the input array has a “0” in its 7th position.)

  • \(3\)
  • \(1\)
  • \(2\)
  • \(4\)

ANSWER: The recursion tree is shown below, solid boxes represent going down into recursion, dashed boxes represent coming up from recursion. Option 3 is correct.

Merge Sort Recursion Tree
Merge Sort Recursion Tree.

What is the asymptotic worst-case running time of MergeSort, as a function of the input array length \(n\)?

  • \(\Theta(n\log n)\)
  • \(\Theta(\log n)\)
  • \(\Theta(n^2)\)
  • \(\Theta(n)\)

ANSWER: Option 1 is correct.

What is the asymptotic running time of Randomized QuickSort on arrays of length \(n\), in expectation (over the choice of random pivots) and in the worst case, respectively?

  • \(\Theta(n\log n)\) [expected] and \(\Theta(n\log n)\) [worst case]
  • \(\Theta(n)\) [expected] and \(\Theta(n\log n)\) [worst case]
  • \(\Theta(n^2)\) [expected] and \(\Theta(n^2)\) [worst case]
  • \(\Theta(n\log n)\) [expected] and \(\Theta(n^2)\) [worst case]

ANSWER: Option 4 is correct. Worst case is when the pivot is always chosen as the first element, thus the problem size reduces by at most \(1\) in each iteration, therefore, number of iterations needed until we hit the base case \(n = 1\) is \(n\). Since partitioning takes linear time in each iteration, the worst case time is quadratic.

Let \(f\) and \(g\) be two increasing functions, defined on the natural numbers, with \(f(1), g(1) \geq 1\). Assume that \(f(n) = O(g(n))\). Is \(2^{f(n)} = O(2^{g(n)})\) (Multiple answers may be correct, check all that apply.)

  • Never
  • Yes if \(f(n) \leq g(n)\) for all sufficiently large \(n\)
  • Maybe, maybe not (depends on the functions \(f\) and \(g\))
  • Always

ANSWER: Options 2 and 4 are correct. See Problem Set 1.

Let \(0 < \alpha < .5\) be some constant. Consider running the Partition subroutine on an array with no duplicate elements and with the pivot element chosen uniformly at random (as in QuickSort and RSelect). What is the probability that, after partitioning, both subarrays (elements to the left of the pivot, and elements to the right of the pivot) have size at least \(\alpha\) times that of the original array?

  • \(2 - 2\alpha\)
  • \(1 - \alpha\)
  • \(1 - 2\alpha\)
  • \(\alpha\)

ANSWER: Option 3 is correct. See Probability Questions.

Suppose that a randomized algorithm succeeds (e.g., correctly computes the minimum cut of a graph) with probability \(p\) (with \(0 < p < 1\)). Let \(\epsilon\) be a small positive number (less than \(1\)). How many independent times do you need to run the algorithm to ensure that, with probability at least \(1 - \epsilon\), at least one trial succeeds?

  • \(\frac{\log \epsilon}{\log p}\)
  • \(\frac{\log(1 - p)}{\log \epsilon}\)
  • \(\frac{\log \epsilon}{\log(1 - p)}\)
  • \(\frac{\log p}{\log \epsilon}\)

ANSWER: Suppose we run the algorithm for \(n\) times and, therefore, the probability for all of these independent trials to fail is \((1 - p)^n\). The probability to success is, therefore:

\[\begin{equation*} \begin{aligned} 1 - (1 - p)^n & \geq 1 - \epsilon \\ (1 - p)^n & \leq \epsilon \text{ (flipping inequality due to change in sign)} \\ n\log(1 -p) & \leq \log \epsilon \end{aligned} \end{equation*}\]

Since, \(1 - p\) and \(\epsilon\) are both less than \(1\), therefore, their logarithms are negative.

\[\begin{equation*} \begin{aligned} n\log(1 -p) & \geq \log \epsilon \text{ (flipping inequality due to change in sign)} \\ n & \geq \frac{\log \epsilon}{\log(1 -p)} \end{aligned} \end{equation*}\]

Suppose you are given \(k\) sorted arrays, each with n elements, and you want to combine them into a single array of \(kn\) elements. Consider the following approach. Divide the \(k\) arrays into \(\frac{k}{2}\) pairs of arrays, and use the Merge subroutine taught in the MergeSort lectures to combine each pair. Now you are left with \(\frac{k}{2}\) sorted arrays, each with \(2n\) elements. Repeat this approach until you have a single sorted array with \(kn\) elements. What is the running time of this procedure, as a function of \(k\) and \(n\)?

  • \(\Theta(nk\log k)\)
  • \(\Theta(nk^2)\)
  • \(\Theta(nk\log n)\)
  • \(\Theta(n\log k)\)

ANSWER: The Merge subroutine takes linear time, so the work done at each iteration is given by subproblem size \(\times\) # of subproblems.

\[\begin{aligned} 2n \times \frac{k}{2} = nk \\ 4n \times \frac{k}{4} = nk \end{aligned}\]

Since \(k\) is halved each time, it’ll take \(\log k\) recursions to reach the base case. Therefore, \(\Theta(nk\log k)\) is the running time. Option 1 is correct.

Running time of Strassen’s matrix multiplication algorithm: Suppose that the running time of an algorithm is governed by the recurrence \(T(n) = 7 * T(\frac{n}{2}) + n^2\). What’s the overall asymptotic running time (i.e., the value of \(T(n)\))?

  • \(\Theta(n^2)\)
  • \(\Theta(n^2\log n)\)
  • \(\Theta(n^{\log_2 7})\)
  • \(\Theta(n^\frac{\log 2}{\log 7})\)

ANSWER: Master Method, \(a = 7, b = 2, d = 2, a > b^d\), case 3, \(O(n^{\log_b a}) = O(n^{\log_2 7})\). Option 3 is correct.

Recall the Master Method and its three parameters \(a, b, d\). Which of the following is the best interpretation of \(b^d\), in the context of divide-and-conquer algorithms?

  • The rate at which the total work is growing (per level of recursion).
  • The rate at which the subproblem size is shrinking (per level of recursion).
  • The rate at which the work-per-subproblem is shrinking (per level of recursion).
  • The rate at which the number of subproblems is growing (per level of recursion).

ANSWER: Option 3 is correct.

Consider a directed graph \(G = (V,E)\) with non-negative edge lengths and two distinct vertices \(s\) and \(t\) of \(V\). Let \(P\) denote a shortest path from \(s\) to \(t\) in \(G\). If we add 10 to the length of every edge in the graph, then: [Check all that apply.]

  • If \(P\) has only one edge, then \(P\) definitely remains a shortest \(s-t\) path.
  • \(P\) definitely remains a shortest \(s-t\) path.
  • \(P\) might or might not remain a shortest \(s-t\) path (depending on the graph).
  • \(P\) definitely does not remain a shortest \(s-t\) path.

ANSWER: Option 1 is trivially correct.

Option 2 is incorrect, see Problem Set 5 for an example.

Option 3 is correct, see Problem Set 4 for an example.

Option 4 is incorrect because it contradicts option 3.

What is the running time of depth-first search, as a function of \(n\) and \(m\), if the input graph \(G = (V,E)\) is represented by an adjacency matrix (i.e., NOT an adjacency list), where as usual \(n = |V|\) and \(m = |E|\) ?

  • \(\Theta(n + m)\)
  • \(\Theta(n * m)\)
  • \(\Theta(n^2)\)
  • \(\Theta(n^2\log m)\)

ANSWER: In order to find the adjacent nodes for a node, we need to look through the entire row of size \(n\). Since there are \(n\) nodes, the running time is clearly quadratic in \(n\). Thus, option 3 is correct.

What is the asymptotic running time of the Insert and Extract-Min operations, respectively, for a heap with \(n\) objects?

  • \(\Theta(1)\) and \(\Theta(\log n)\)
  • \(\Theta(\log n)\) and \(\Theta(\log n)\)
  • \(\Theta(n)\) and \(\Theta(1)\)
  • \(\Theta(\log n)\) and \(\Theta(1)\)

ANSWER: Option 2 is correct. See leature video 12.2 for proofs.

On adding one extra edge to a directed graph \(G\), the number of strongly connected components…?

  • …might or might not remain the same (depending on the graph).
  • …cannot change.
  • …cannot decrease by more than one.
  • …cannot decrease

ANSWER: Option 1 is correct, see Problem Set 4 for an example.

Which of the following statements hold? (As usual \(n\) and \(m\) denote the number of vertices and edges, respectively, of a graph.) [Check all that apply.]

  • Breadth-first search can be used to compute shortest paths in \(O(m + n)\) time (when every edge has unit length).
  • Depth-first search can be used to compute a topological ordering of a directed acyclic graph in \(O(m + n)\) time.
  • Depth-first search can be used to compute the strongly connected components of a directed graph in \(O(m + n)\) time.
  • Breadth-first search can be used to compute the connected components of an undirected graph in \(O(m + n)\) time.

ANSWER: All of the options are true as explained below:

  1. If every edge has unit length, ignore the edge lengths, and run BFS from a single source vertex \(s\). Stop when the vertex dequeued is the destination vertex \(t\). \(O(m + n)\).
  2. Run DFS, but instead of outputting a vertex as soon as it’s visited, put it on a stack after all of its adjacent vertices have been visited. In other words, do a reverse-postorder traversal. \(O(m + n)\).
  3. Kosaraju’s algorithm. \(O(m + n)\).
  4. Kosaraju’s algorithm can also be implemented by BFS as long as the post-order property is preserved. (TBD: implement).

When does a directed graph have a unique topological ordering?

  • Whenever it is directed acyclic
  • None of the other options
  • Whenever it is a complete directed graph
  • Whenever it has a unique cycle

ANSWER: 3. From here “a digraph has a unique topological ordering if and only if there is a directed edge between each pair of consecutive vertices in the topological order (i.e., the digraph has a Hamiltonian path).” (Why?)

Suppose you implement the operations Insert and Extract-Min using a sorted array (from biggest to smallest). What is the worst-case running time of Insert and Extract-Min, respectively? (Assume that you have a large enough array to accommodate the Insertions that you face.)

  • \(\Theta(n)\) and \(\Theta(n)\)
  • \(\Theta(1)\) and \(\Theta(n)\)
  • \(\Theta(\log n)\) and \(\Theta(1)\)
  • \(\Theta(n)\) and \(\Theta(1)\)

ANSWER: See Problem set 5.

Which of the following patterns in a computer program suggests that a heap data structure could provide a significant speed-up (check all that apply)?

  • Repeated maximum computations
  • None of the other options
  • Repeated minimum computations
  • Repeated lookups

ANSWER: Options 1 and 3 are what heaps are good for.

Which of the following patterns in a computer program suggests that a hash table could provide a significant speed-up (check all that apply)?

  • None of the other options
  • Repeated maximum computations
  • Repeated lookups
  • Repeated minimum computations

ANSWER: Option 3 is what a hash table is good for.

Which of the following statements about Dijkstra’s shortest-path algorithm are true for input graphs that might have some negative edge lengths? [Check all that apply.]

  • It is guaranteed to terminate.
  • It is guaranteed to correctly compute shortest-path distances (from a given source vertex to all other vertices).
  • It may or may not terminate (depending on the graph).
  • It may or may not correctly compute shortest-path distances (from a given source vertex to all other vertices), depending on the graph.

ANSWER: Dijkstra’s algorithm is guaranteed to terminate in grapgs that don’t have negative weight cycles; thus, option 1 is correct.

Nonnegativity of the edge lengths was used in the correctness proof for Dijkstra’s algorithm; with negative edge lengths, the algorithm is no longer correct in general. Thus, option 2 is incorrect.

Option 3 is incorrect because it contradicts option 1.

Option 4 is correct.

Updated:

Leave a comment

You may also enjoy