Problem Set 2
Suppose we are given a directed graph \(G (V,E)\) in which every edge has a distinct positive edge weight. A directed graph is acyclic if it has no directed cycle. Suppose that we want to compute the maximum-weight acyclic subgraph of \(G\) (where the weight of a subgraph is the sum of its edges’ weights). Assume that \(G\) is weakly connected, meaning that there is no cut with no edges crossing it in either direction.
Here is an analog of Prim’s algorithm for directed graphs. Start from an arbitrary vertex \(s\), initialize \(S = \{s\}\) and \(F = \emptyset\). While \(S \neq V\), find the maximum-weight edge \((u,v)\) with one endpoint in \(S\) and one endpoint in \(V -S\). Add this edge to \(F\), and add the appropriate endpoint to \(S\).
Here is an analog of Kruskal’s algorithm. Sort the edges from highest to lowest weight. Initialize \(F=\emptyset\). Scan through the edges; at each iteration, add the current edge \(i\) to \(F\) if and only if it does not create a directed cycle.
Which of the following is true?
- Both algorithms might fail to compute a maximum-weight acyclic subgraph.
- Only the modification of Kruskal’s algorithm always computes a maximum-weight acyclic subgraph.
- Only the modification of Prim’s algorithm always computes a maximum-weight acyclic subgraph.
- Both algorithms always compute a maximum-weight acyclic subgraph.
ANSWER: Consider the two-node graph \(A \xrightarrow{10} B \xrightarrow{6} A, B \xrightarrow{7} A\) (yes, two edges from \(B\) to \(A\); nothing in the question precludes that). Analog of Prim’s creates a cycle no matter which vertex it chooses first. Analog of Kruskal’s chooses \(A \rightarrow B\) and then halt. However, the maximum-weight acyclic subgraph consists of the two edges \(B \rightarrow A\) which either algorithms fails to find. Thus, option 1 is correct.
Consider a connected undirected graph \(G\) with edge costs that are not necessarily distinct. Suppose we replace each edge cost \(c_e\) with \(-c_e\); call this new graph \(G'\). Consider running either Kruskal’s or Prim’s minimum spanning tree algorithm on \(G'\), with ties between edge costs broken arbitrarily, and possibly differently, in each algorithm. Which of the following is true?
- Both algorithms compute the same maximum-cost spanning tree of \(G\).
- Both algorithms compute a maximum-cost spanning tree of \(G\), but they might compute different ones.
- Prim’s algorithm computes a maximum-cost spanning tree of \(G\) but Kruskal’s algorithm might not.
- Kruskal’s algorithm computes a maximum-cost spanning tree of \(G\) but Prim’s algorithm might not.
ANSWER: Option 2 is correct; different tie-breaking rules may yield different spanning trees.
Consider the following algorithm that attempts to compute a minimum spanning tree of a connected undirected graph \(G\) with distinct edge costs. First, sort the edges in decreasing cost order (i.e., the opposite of Kruskal’s algorithm). Initialize \(T\) to be all edges of \(G\). Scan through the edges (in the sorted order), and remove the current edge from \(T\) if and only if it lies on a cycle of \(T\).
Which of the following statements is true?
- The output of the algorithm will never have a cycle, but it might not be connected.
- The algorithm always outputs a spanning tree, but it might not be a minimum cost spanning tree.
- The output of the algorithm will always be connected, but it might have cycles.
- The algorithm always outputs a minimum spanning tree.
ANSWER: During the iteration in which an edge is removed, it was on a cycle \(C\) of \(T\). By the sorted ordering, it must be the maximum-cost edge of \(C\). By an exchange argument, it cannot be a member of any MST. Since every edge deleted by the algorithm belongs to no MST, and its output is a spanning tree (no cycles by construction, connected by the Lonely Cut Corollary), its output must be the (unique) MST. Therefore, option 4 is correct.
You are given a connected undirected graph \(G\) with distinct edge costs, in adjacency list representation. You are also given the edges of a minimum spanning tree \(T\) of \(G\). This question asks how quickly you can recompute the MST if we change the cost of a single edge. Which of the following are true? [RECALL: It is not known how to deterministically compute an MST from scratch in \(O(m)\) time, where \(m\) is the number of edges of \(G\).] [Check all that apply.]
- Suppose \(e \in T\) and we increase the cost of \(e\). Then, the new MST can be recomputed in \(O(m)\) deterministic time.
- Suppose \(e \notin T\) and we increase the cost of \(e\). Then, the new MST can be recomputed in \(O(m)\) deterministic time.
- Suppose \(e \in T\) and we decrease the cost of \(e\). Then, the new MST can be recomputed in \(O(m)\) deterministic time.
- Suppose \(e \notin T\) and we decrease the cost of \(e\). Then, the new MST can be recomputed in \(O(m)\) deterministic time.
ANSWER: Option 1: Let \(A,B\) be the two connected components of \(T - \{e\}\). Edge \(e\) no longer belongs to the new MST if and only if it is no longer the cheapest edge crossing the cut \((A,B)\) (this can be checked in \(O(m)\) time). If \(f\) is the new cheapest edge crossing \((A,B)\), then the new MST is \(T - \{e\} \cup \{f\}\).
Option 2 and 3: The MST does not change, so no re-computation is needed.
Option 4: Let C be the cycle of \(T \cup \{e\}\). Edge \(e\) belongs to the new MST if and only if it is no longer the most expensive edge of \(C\) (this can be checked in \(O(m)\) time). If \(f\) is the new most expensive edge of \(C\), then the new MST is \(T \cup \{e\} - \{f\}\).
Thus, all four options are correct.
Consider an alphabet with five letters, \(\{a,b,c,d,e\}\), and suppose we know the frequencies \(f_a = 0.32, f_b = 0.25, f_c = 0.2, f_d = 0.18, \text{ and } f_e = 0.05\). What is the expected number of bits used by Huffman’s coding scheme to encode a 1000-letter document?
- 3450
- 2400
- 3000
- 2230
ANSWER: Recall from lecture video 8.3, the average encoding length \(L(T)\) is given by \(\sum_{i \in \Sigma} (P_i \cdot [\text{depth of i in T}])\). A binary tree for the alphabet in question is given below.
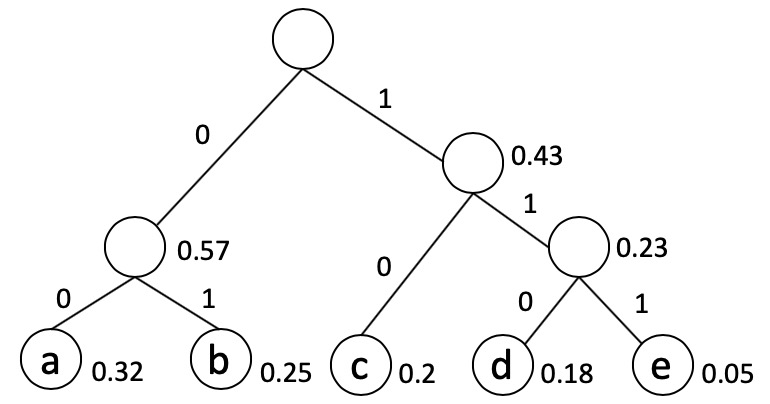
Therefore, for a 1000-letter document, the expected number of bits is \(2230\). Option 4 is correct.
Which of the following statements holds for Huffman’s coding scheme?
- If the most frequent letter has frequency less than \(0.5\), then all letters will be coded with more than one bit.
- A letter with frequency at least \(0.5\) might get encoded with two or more bits.
- If a letter’s frequency is at least \(0.4\), then the letter will certainly be coded with only one bit.
- If the most frequent letter has frequency less than \(0.33\), then all letters will be coded with at least two bits.
ANSWER: Option 1 is incorrect; counterexample: Frequencies 0.49, 0.48, and 0.3.
Option 2 is incorrect. A letter with frequency at least \(0.5\) is going to be the last one to be merged, because there cannot be any other letter with higher frequency.
Option 3 is incorrect; counterexample: Frequencies 0.4, 0.4, and 0.2.
Option 4 is correct. Such a letter will endure a merge in at least two iterations: the last one (which involves all letters), and at least one previous iteration. In the penultimate iteration, if the letter has not yet endured a merge, at least one of the two other remaining subtrees has cumulative frequency at least \(\frac{1 - 0.33}{2} \gt 0.33\), so the letter will get merged in this iteration.
Under a Huffman encoding of \(n\) symbols, how long (in terms of number of bits) can a codeword possibly be?
- \(ln \ n\)
- \(n - 1\)
- \(n\)
- \(\log_2 n\)
ANSWER: Consider the frequencies \(2, 4, 8, 16\) (powers of two). Clearly, \(2\) (and \(4\)) participates in every merge, of which, there are three (in general, \(n - 1\)). Therefore, option 2 is correct.
Option 1 is the best-case scenario.
This problem is not unique to Huffman encoding, it’s the case of an unbalanced Binary Tree devolving into a linked list.

Comments